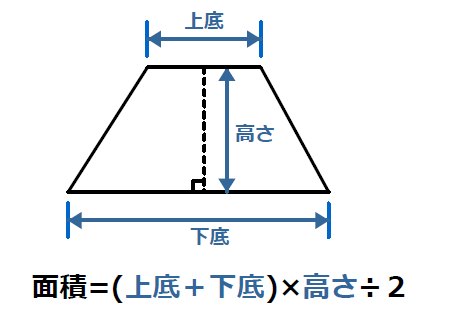
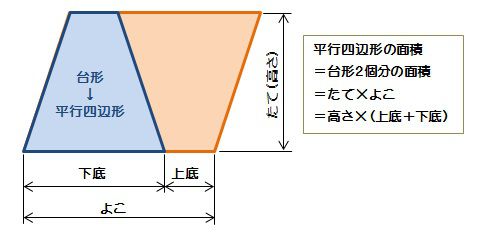
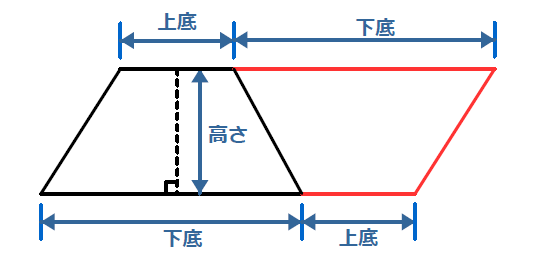
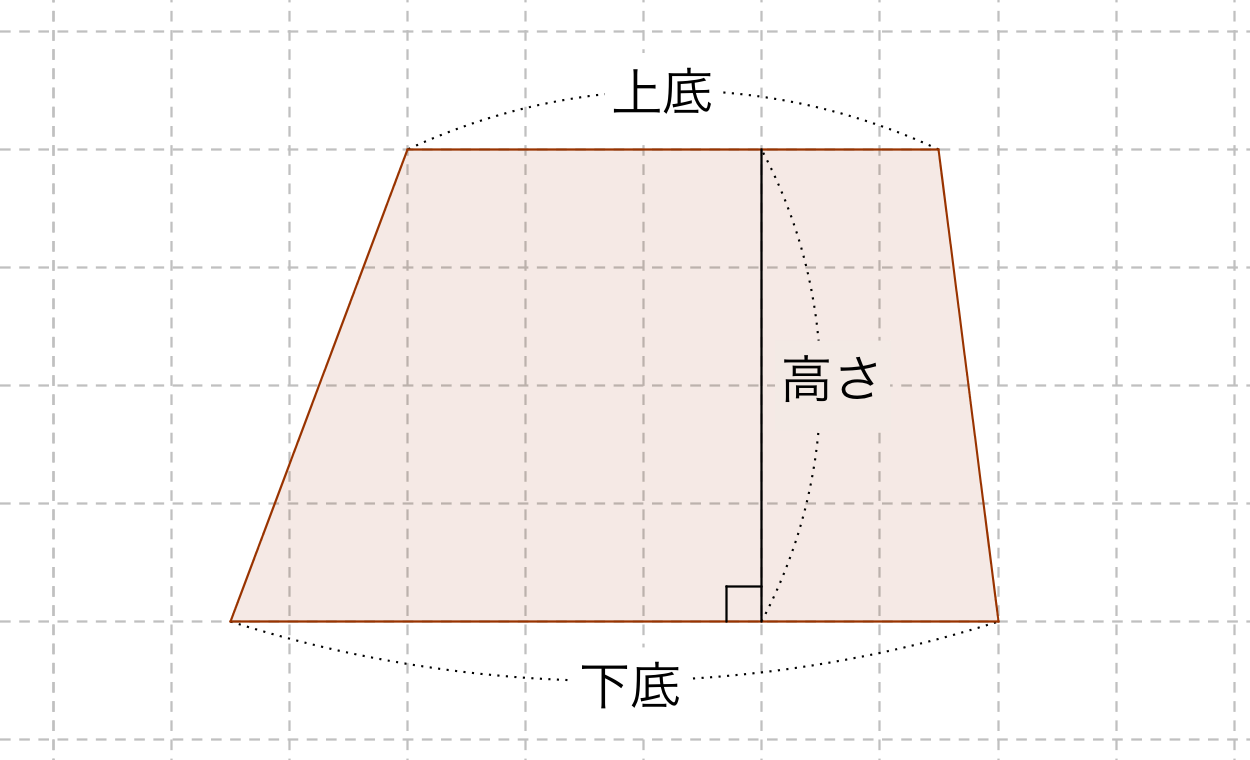
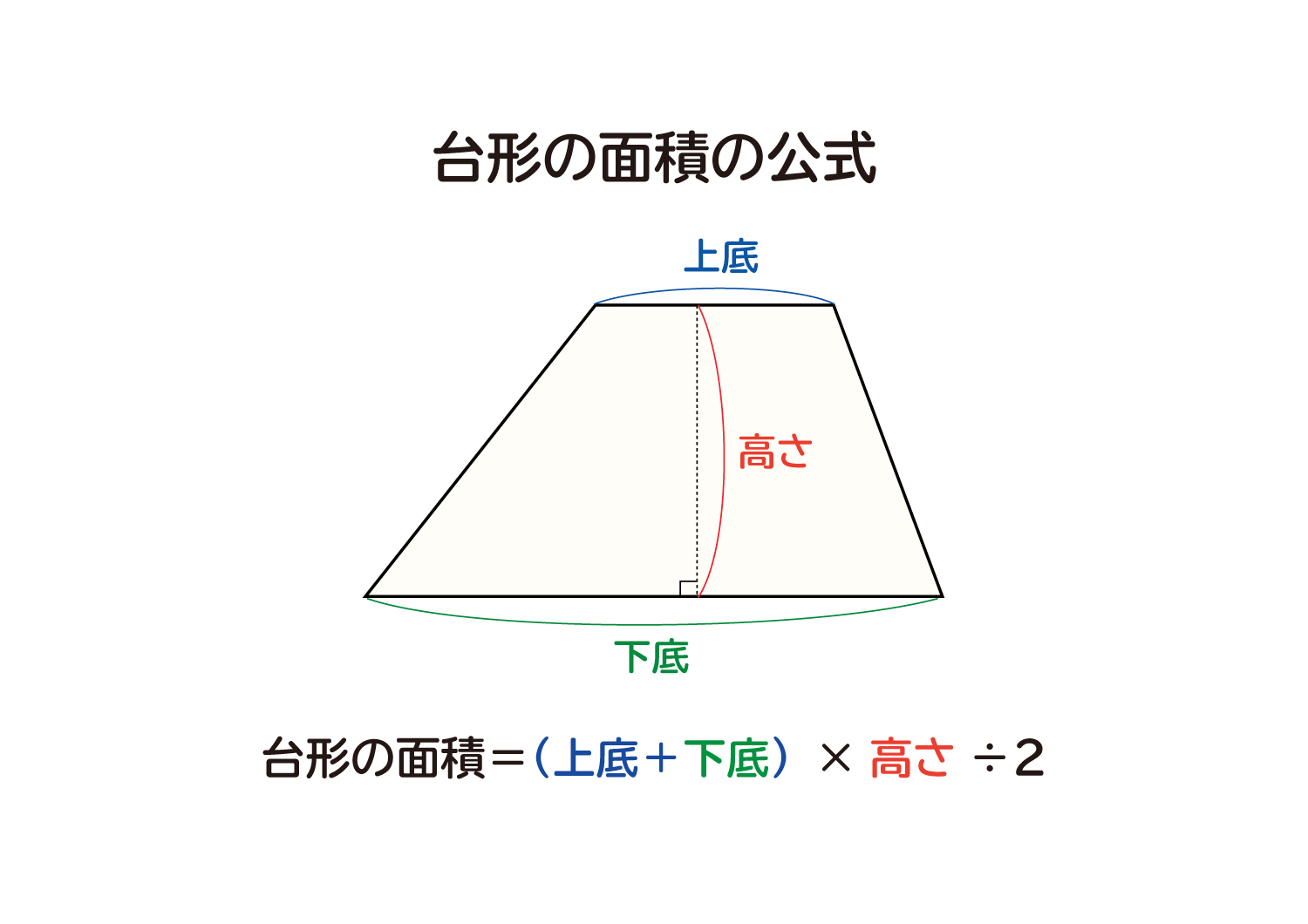
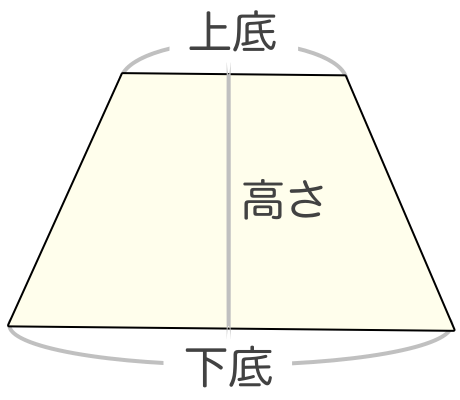
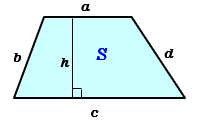
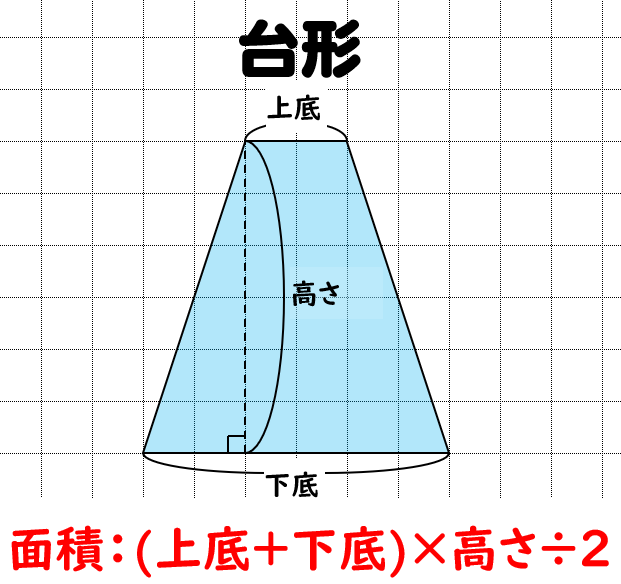
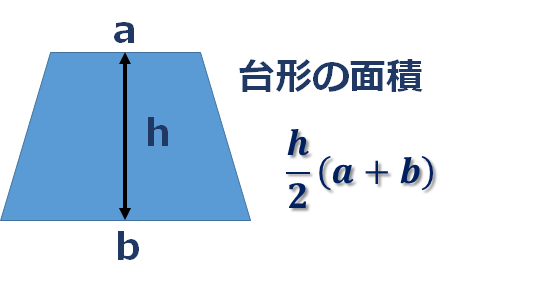
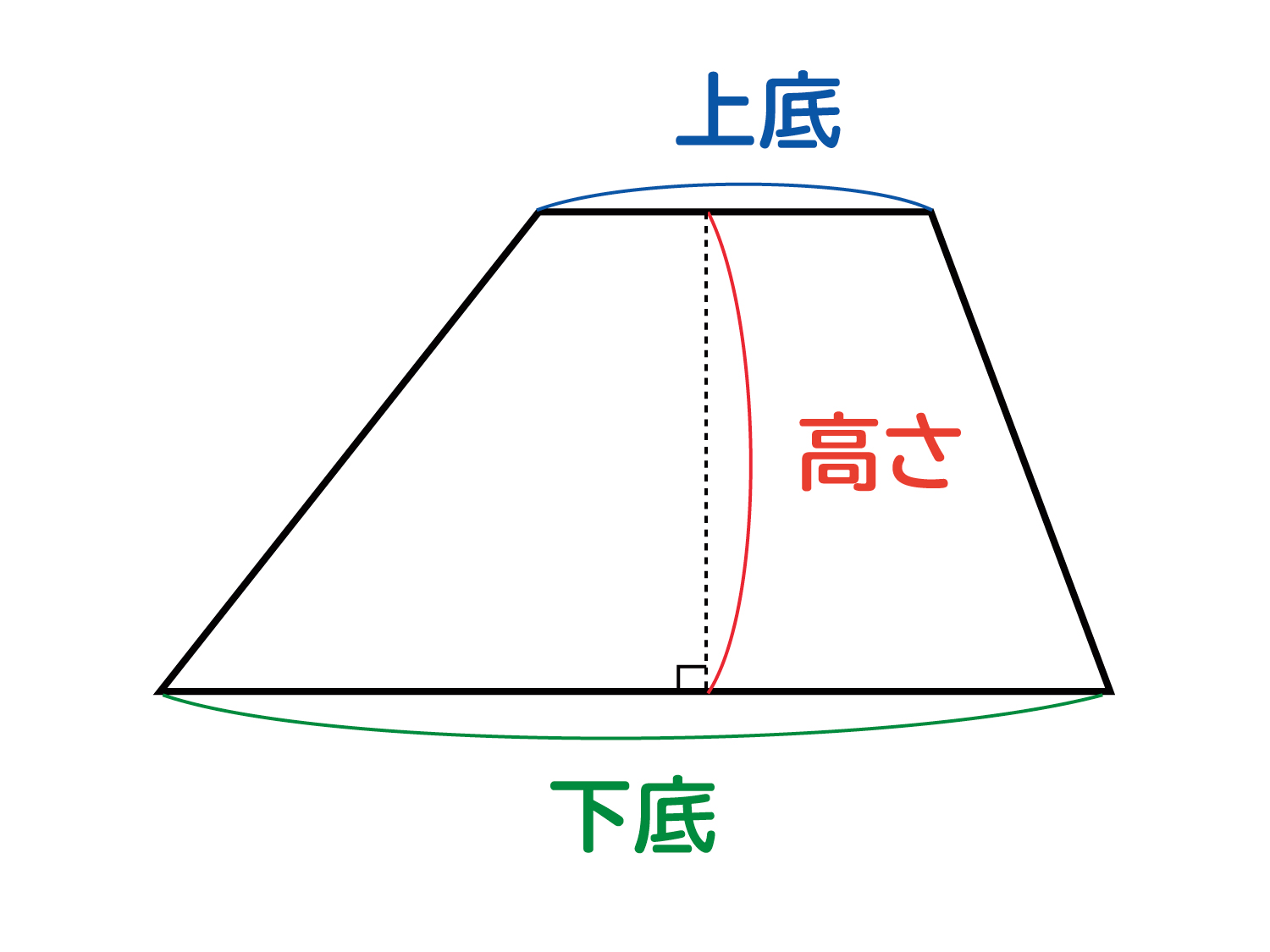
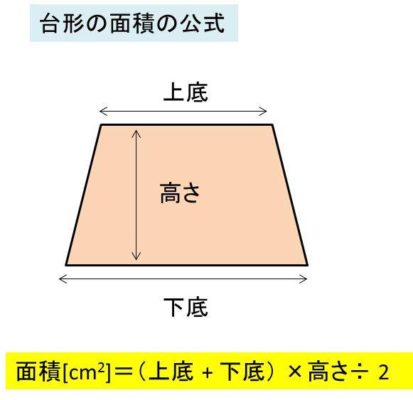
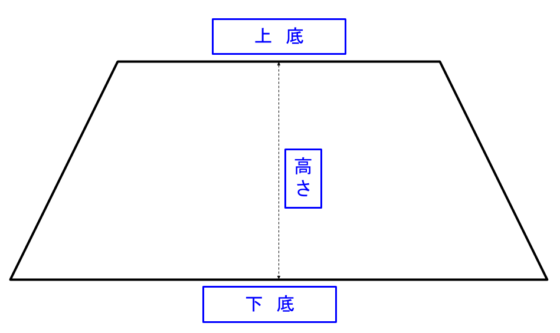
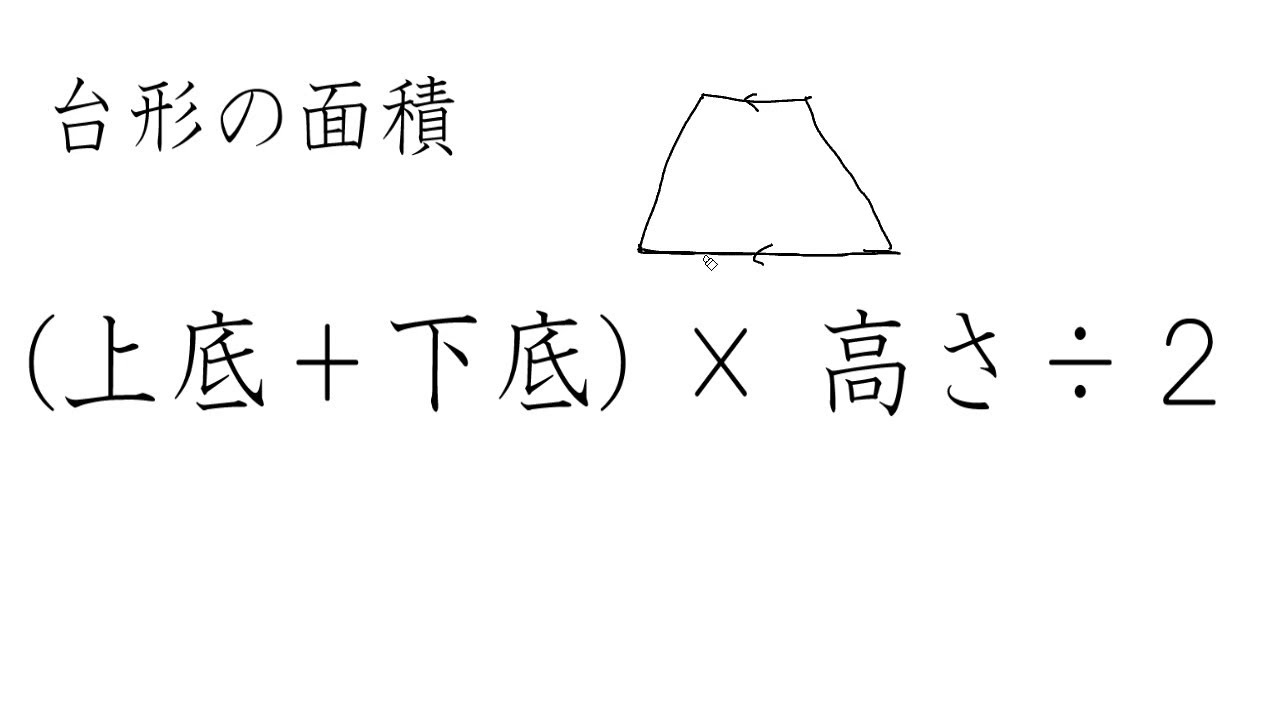
台形の面積を求める公式は 台形の面積 上底 下底 高さ 台 形 の 面 積 = (上 底 下 底) × 高 さ ÷ 2よく知られているように積分の計算はむつかしい。定積分を数値的に近似計算することを数値積 分という。 この文書では、主に1 次元の定積分 I = ∫b a f(x)dx (1 a < b 1) の計算法について説明する。台形 面積計算 公式 求め方 高さ 上底 足す 下底 自動 割る area 面積 台形 面積;
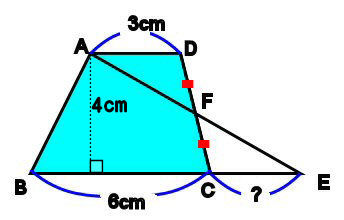
台形と三角形
台形 計算 の 仕方
台形 計算 の 仕方-Q台形ねじ技術計算 1接触面圧P、2すべり速度V算出 pv 値グラフより p、v の交点が内側にあるか確認 使用条件の決定 軸方向荷重、回転数 台形ねじナット型式の仮決定 台形ねじナット材質 3ねじ効率η、4負荷トルクt の算出 モータ等の選定に使用 ng台形法に似た計算方法に中点法(midpoint method)がある。そのアイデアは単純で、短冊の面積を中点の関数値を使って $$ f\left(\frac{x_i x_{i1}}{2}\right) \Delta x $$ で近似するというものだ($\Delta x$は短冊の幅)。台形法のプログラムを元に、中点法のコードを作成し、動作を確認してみ
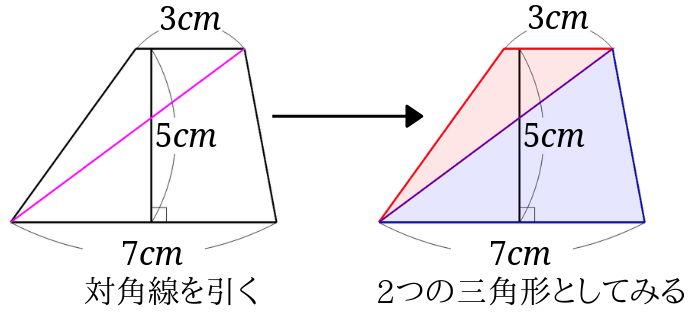



台形の面積は公式が分からなくても大丈夫 対角線を引いたり等積変形を利用したりする求め方とは みけねこ小学校
ソフト名: 流量計算「Flow2」(台形、円形) フリー版 ファイル: flow2_fzip / 2,609,168Bytes / 流量計算「Flow2」(台形、円形) フリー版 を今すぐダウンロード みんなで共有 追加説明 動作に 台形の面積の公式 台形の面積を 、高さを 、上底を 、下底を とすると、 (台形の面積) (上底 下底) (高さ)比べる図形が相似であれば、相似比を2乗することで面積比を求めることができます。 つまり、台形の中から相似な図形を見つけていくことがポイントになってくるね。 相似な図形において、面積比は相似比の2乗になる 比べる三角形が相似でなくても
台形則 St S =∫ b a f(x)dx (1) T rapezoid St = h 2{f(a)2n−1 ∑ j=1f(ajh)f(b)}, h = b−a n S = ∫ a b f ( x) d x ( 1) T r a p e z o i d S t = h 2 { f ( a) 2 ∑ j = 1 n − 1 f ( a j h) f ( b) }, h = b − a n お客様の声 アンケート投稿台形計算, 台形速度の軌跡生成をしてロボットを制御する方 台形速度プロファイルは、全部で3つの期間 加速期間(t 1 ) 巡航期間(t 2 ) 減速期間(t 3 ) で生成されています。 この台形速度プロファイルを作成するため、必要となるパラメータ(t 1 、t 2 、t 3 )を求めます。 パラメータのねじリード角の計算方法 α:リード角 I:リード n:条数 P:ピッチ d:ねじの有効径 下の空欄を全て埋めてください。 ねじ種類1 ねじ種類2 有効径 mm 計算方法 ピッチ 条数 リード インサート
流量計算「Flow2」(台形、円形) フリー版 のダウンロードファイル情報;台形の面積 A: B: H: 面積: 円 円 半円 扇形 円周長から面積 四角形 四角形 四角形 4辺と対角線 角パイプ 三角形 三角形 三角形(3辺) 四角形 平行四辺形 ひし形 台形 LC形 L形 C形 円形「台形」の面積計算ドリル/ 問題集 小学校5年生で習う「台形」の面積を求める問題集です。 問題をランダムで生成することができ、答えの表示・非表示も切り替えられます。印 小学校算数の目次 小学5年生 POSTED COMMENT あむ より 2月 10, 19 1250 pm 高さ3センチなのになぜ6になるの
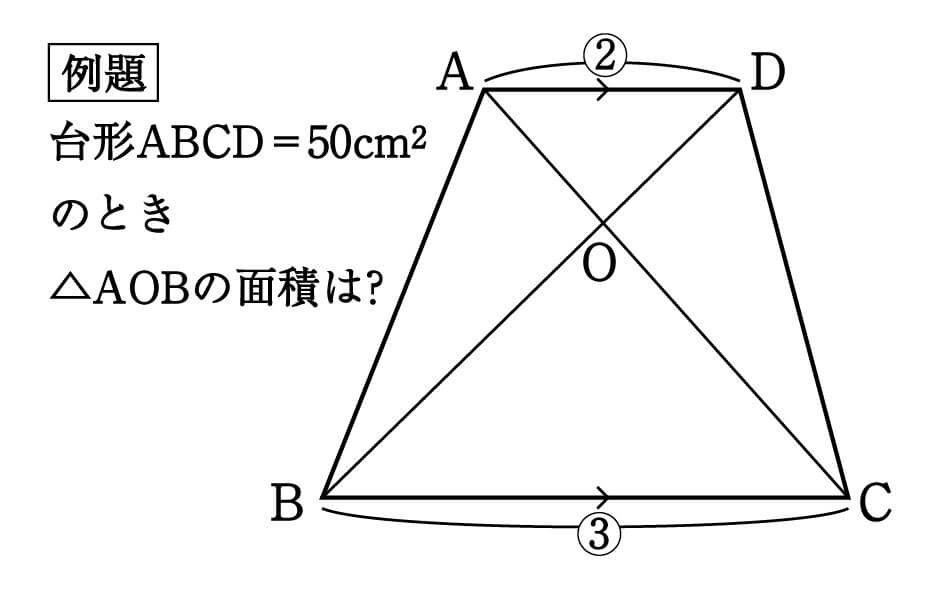



数学 台形を4分割した図形パターン 面積比 集中特訓 3 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




小5 台形 面積の求め方 日本語版 Youtube
台形ねじ・三角ねじの場合 角ねじの場合は斜面が水平でしたから、計算は簡単でした。 では台形ねじや三角ねじの様に頂角が30°や60°の場合はどうしたらよいでしょうか? 図5を見ると角ねじの場合の推力Q1がQ1'に減っています。 その関係は、Excelで関数を積分する2(台形公式) 積分はグラフの領域の面積を求める計算になる。 これも正確には計算できないが、領域を長方形に分割して合計すれば、多少不正確であっても計算できる。 分割を細かくすると、値は正確になる。 また、長方形を使うのではなく、台形を使えばより正確に注意:最後の台形は、曲線の下でx = 14からx = 15の間にあります。 したがって、以下のスクリーンショットに示すように、オートフィルハンドルを最後からXNUMX番目のセルにドラッグします。 3。 これで、すべての台形の面積が計算されました。



台形の面積計算 ゆるゆるプログラミング



台形の面積の計算 の解答と解説 多目的ルーム 楽天ブログ
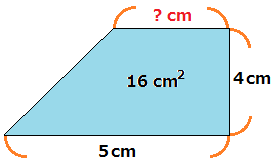
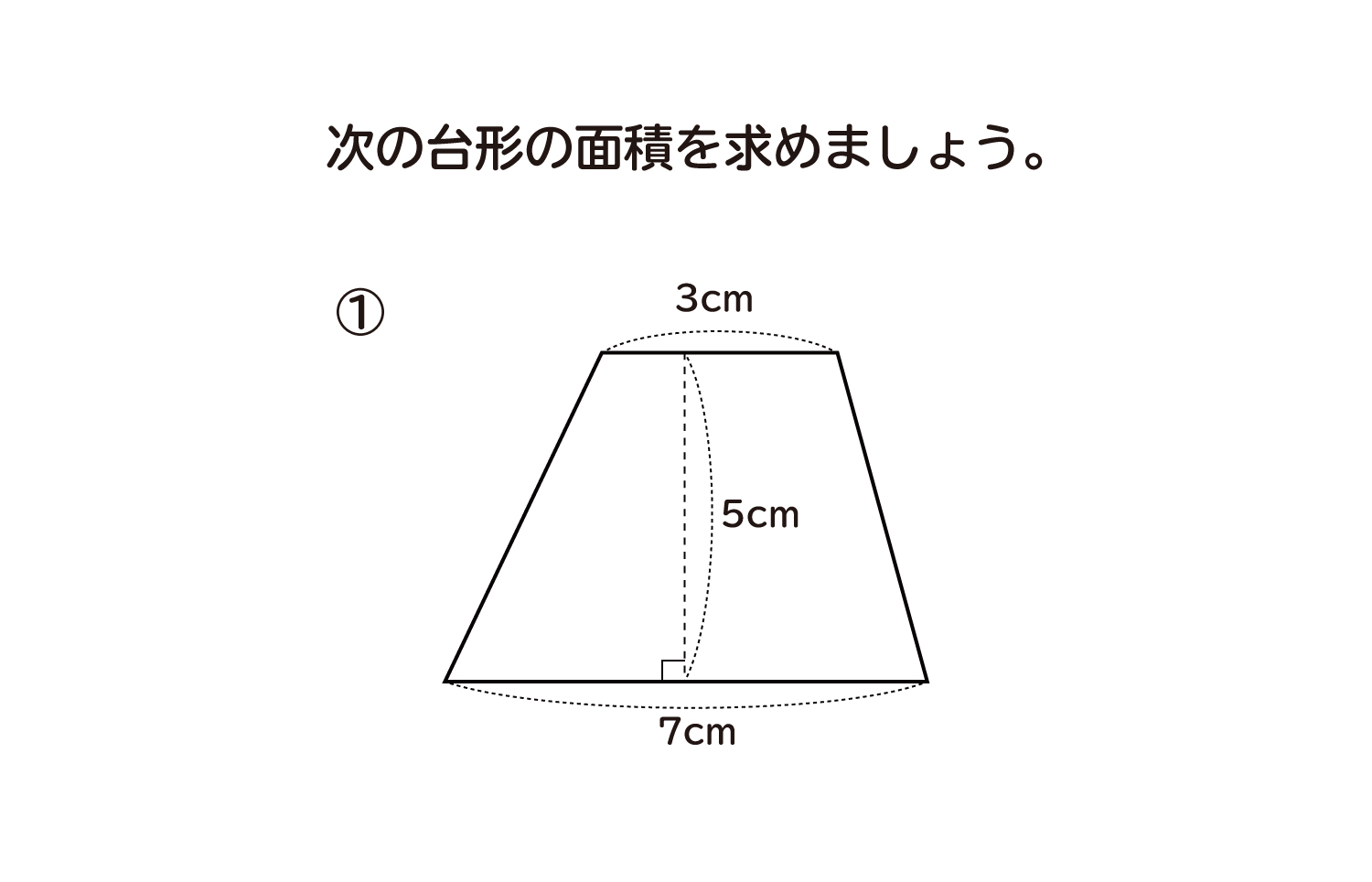
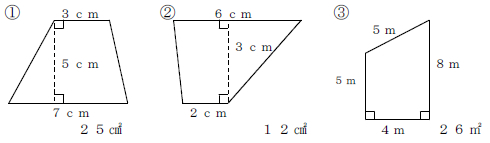
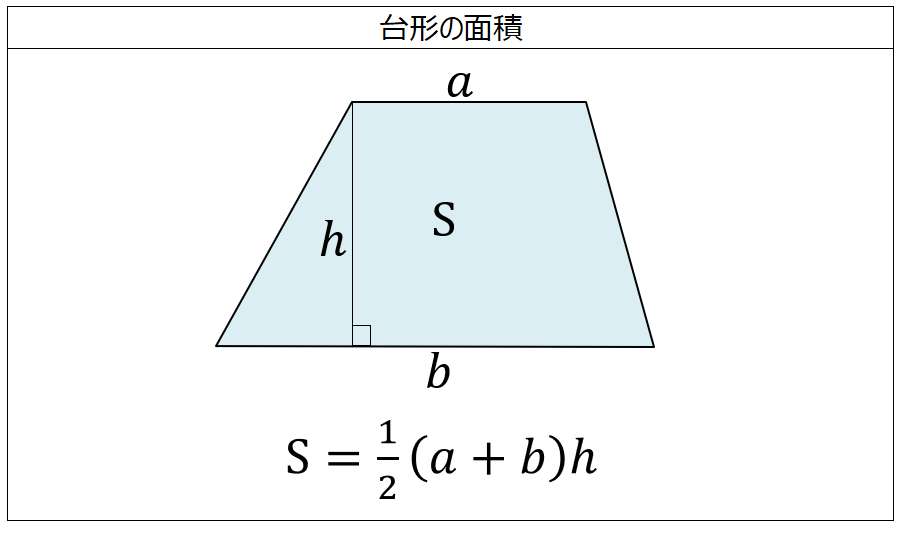
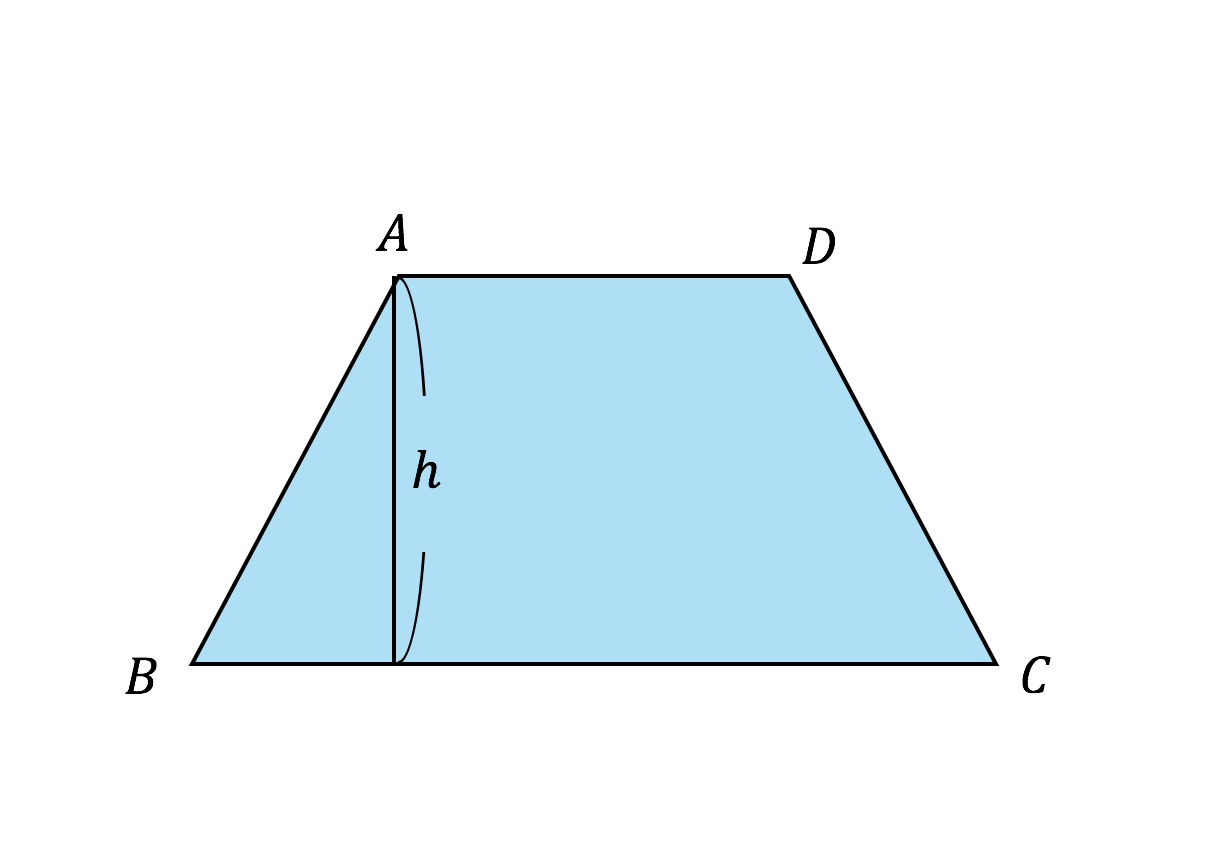
台形の面積=(上底+下底)×高さ÷2 で求めることができます。 この換算式に慣れるためにも計算問題にチャレンジしてみましょう。 例題1 上底が3cm、下底が5cm、高さ2cmの台形の面積を計算してみましょう。 解答1 上述の定義に従い計算します。 地道に計算してやると、 (正四角錐iabcd) (正四角錐iefgh) = 1/3 × ( 66) × 4^2 – 1/3 ×6 × 2^2 = 64 – 8 = 56cm^3 になる。 おめでとう! これで台形の体積、、じゃなくて、 正四角錐台の体積を計算できたね!! まとめ:台形の体積の求め方は「上 – 下」!台形断面の等流計算 開水路の等流計算には、次のマニングの公式がよく用いられる。 (式-2) 補足 (上底+下底)×高さ÷2 で上底= として整理する。 ここで、各記号は次のことを示している。 n:粗度係数(水路壁面、底面の粗さを示す値で、水路の材質や状態により異なる。 ) R:径深(水理学的平均水深とも言う。 流積を潤辺で割ったもの) S:潤辺



シンプルで難しい問題 台形の面積を求めよ 勉強 Youtube スタディチューブ




面積 の計算 台形 中学受験シリーズ Mayutyanngooのブログ
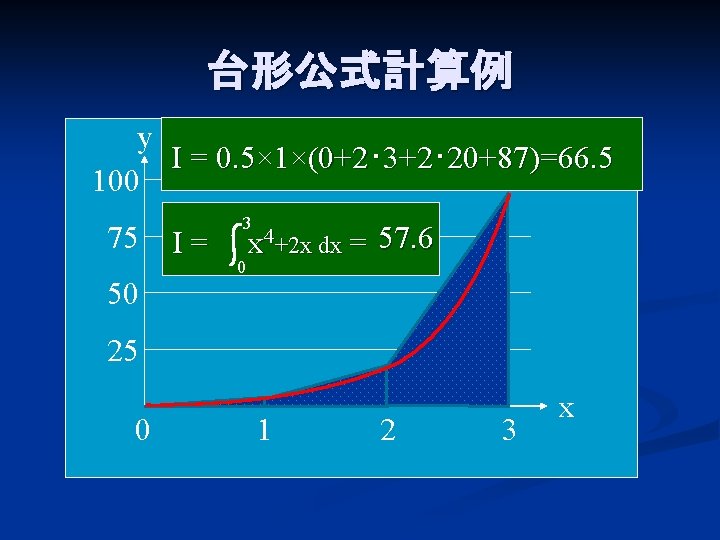
公式計算 平面図形の面積(A),周長(L)および重心位置(G) P11 三角形(a・b・c) P11 三角形(b・c・α) P11 三角形(a・b・h) P11 平行四辺形 P11 台形 P11 四辺形 P11 正n角形 P11 円 P11 扇形 P11 弓形 P11 楕円 P11 放物形 P11 平面図形の性質 P12台形公式による数値積分 漸増計算 台形公式の漸増法 分割数n での台形公式による近似 h= b¡a n Sn = 1 2 f(a) n∑¡1 j=1 f(xjh) 1 2 f(b)£h 分割数2n での台形公式による近似 h0 = b¡a 2n = h 2 S2n = 1 2 f(a) 2∑n¡1 j=1 f(xjh0) 1 2 f(b) £h0 = 1 2 f(a) n∑¡1 k=1 f(x(2k)h0) ∑n k=1 f(x(2k¡1)h0) 1 2 f(b) £h0 = 1 2 f(a) 台形 (だいけい、 積分の数値計算 ではグラフ上のある区間の面積 を求めるために、x 軸、x = a、x = b とグラフで囲まれた図形を有限個の(できるだけ多い)台形で分割し、台形の面積の公式を用いて近似値を得ることがある。台形公式を参照のこと。 関連項目 ポータル 数学 最終更新



台形の面積 算数の公式覚えてますか




高さがわからない台形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
数値積分(台形公式) 微分とは異なり、一般に積分は解析的には求まらないので、 数値計算に頼る必要がでてくる。特異点のない場合、次の(閉じた) 台形公式により、数値積分ができる。 台形則で円周率を計算 では台形則で円周率を計算してみましょう。 区分求積法では赤い部分の面積は長方形の面積の和になっていましたが、 台形則では台形の面積の和になっています。 各台形は上底\(f(x)\),下底\(f(x\frac{1}{n})\),高さ\(\frac{1}{n}\)の台形となっていますから、 次の式で赤い部分の台形の面積を求める公式は、s = {(上底)(下底)}×(高さ)÷2 で表されます。このページでは、台形の面積の求め方を、計算問題と共に説明しています。また、公式の導き方も説明しています。




四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ




台形の 面積 底辺 角度 から上辺 高さを計算したい その2 先 数学 教えて Goo
問題 台形の面積 の解き方を覚えて計算力をつける為に、次の台形の問題を計算しましょう。 問1. 台形とはどんな図形のことをいいますか? 問2. 平行とはどういう意味ですか? 問3. 台形の面積を求める式を答えましょう。 問4.台形の底辺と計算(求め方)、上辺の関係 台形の底辺は、 高さ 面積 上底(または下底) が既知のとき計算できます。これは台形の面積を求める式が、 台形の面積=(上底下底)×高さ÷2 のためです。実際に、下図の台形の底辺(下底)を計算します。の値を台形公式とシンプソンの公式により計算するプログラムを作成 せよ。厳密値πからの誤差も表示せよ。 ヒント:台形公式だけならこうなる。 dx x S ³ 1 1 0 1 2 4 implicit real*8 (ah,oz) f(x)=40d0/(10x*x) pi=40*atan(10d0) write(6,*) „Enter n‟ read(5,*) n a=00d0 b=10d0 h=(ba)/n s=00d0 do 10 k=1, n1 s=sf(ah*k) 10



教育ニュース 台形の面積計算を小学校で習っていないってどういうこと 感謝の心を育むには



台形の面積計算 ゆるゆるプログラミング
台形駆動・三角駆動とは 台形駆動・三角駆動とは、モータを位置決めさせる際の加減速手法のひとつです。 モーションコントロールに於いて、A点からB点に移動させる場合。 計算結果は理論上では限りなく∞(無限大)となりかなりの振動・衝撃となり台形の面積=(上底下底)×高さ÷2ですね。 平行な2つの辺のうち、どちらを上底、下底としてもよいので、 4と6が入れかわっていても間違いではありません。 ただし、学校によっては決められた順番どおりに式を書いていないと 減点する場合があります 台形駆動の計算式 ステッピングモータを台形駆動させるための 計算式のページ を公開しました。 実際はここにあげた数式だけで動かすことは難しいのですが、元となった論文へのリンクと私が使用した計算ファイルを同時に公開していますので、自分でプログラムを作成したい方はそちらを参考にご検討されるのがよいと思います。




台形の面積の求め方 公式と計算例




台形のxを求めたいのですが 計算が合いません Okwave
台形の面積 台形の高さ・面積(4辺の長さから) 台形の1辺・面積(3辺の長さと高さから) ひし形の面積 平行四辺形の面積(底辺と高さから) 平行四辺形の面積(2辺と夾角から) 円に内接する四角形の面積(4辺から) 四角形の面積(4辺と対角の和から)(区分求積法,台形公式,シンプソン公式) 情報数学C (GC) 2 今回の講義内容 今日の問題 区分求積法と台形公式 シンプソン公式 ロンバーグ法 ガウス型積分公式 重積分,モンテカルロ積分 情報数学C (GC) 3 今回の講義で解く問題 න 情報数学C (GC) 4 についての方程式 を区間 , で積分し



台形の面積の公式 算数の公式



台形の面積の計算 自動計算サイト




台形ねじ技術計算 Faメカニカル標準部品 Misumi Vona ミスミの総合webカタログ



台形の面積が苦手 を克服する方法 中学受験ナビ




台形の面積の公式 ゆとり教育で求め方がわからない人は見て 中学や高校の数学の計算問題



なぜ 台形の面積は 上底 下底 高さ 2 なのか を説明します おかわりドリル



台形の面積 簡単に計算できる電卓サイト



小学5年生 算数 無料問題集 台形の面積 おかわりドリル



第5学年 面積 台形 私の実践 私の工夫アーカイブ一覧 授業支援 サポート資料 算数 小学校 知が啓く 教科書の啓林館




面積 下 台形 ひし形 たこ形の面積 面積から辺の長さを求める問題など 思考力算数練習張シリーズ 40 M Access 本 通販 Amazon



相似な図形 計算 台形 練習問題 苦手な数学を簡単に
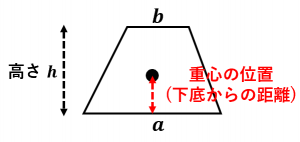



台形の重心を求める公式と導出 具体例で学ぶ数学




台形の面積の求め方 公式と計算例



3



面積の計算 台形 製品設計知識



I 0 5h Y 0y 1y 1y 2




台形の高さを計算するタスクのイラスト素材 ベクタ Image




台形の面積の求め方 公式と計算例




小学5年生 算数 11月 台形の面積 いろいろな図形の面積 割合 百分率の意味と求め方 練習問題プリント 栄光ゼミナール ちびむすドリル 小学生学習教材 スペシャルコラボ




台形の面積の求め方 公式が誰でも一目でわかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ



この台形の求め方を教えて下さい 台形の高さが知りたいです Yahoo 知恵袋



3分で分かる 台形の面積の求め方 公式についてわかりやすく 合格サプリ
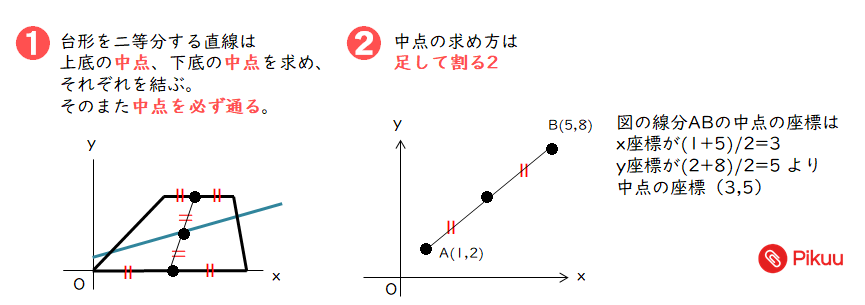



中学数学 二次関数の台形の二等分線を求める練習問題 Pikuu



台形の1辺 面積 3辺の長さと高さから 高精度計算サイト



平面図形の性質 台形の性質 P12




高さがわからない台形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



台形の面積の公式 小学生に教えるための分かりやすい解説 数学fun




台形の面積の求め方 公式 小学生 中学生の勉強




台形 仕事 側 計算 見つけること 台形 問題 側 Canstock




わかった 動いた Pythonで計算問題に挑戦だ 楓プログラミングスタジオ たっきーblog




四角錐台の体積 高精度計算サイト




台形と三角形




台形の面積の求め方 公式 小学生 中学生の勉強




台形 問題 対角線 計算 見つけること 台形 問題 対角線 Canstock
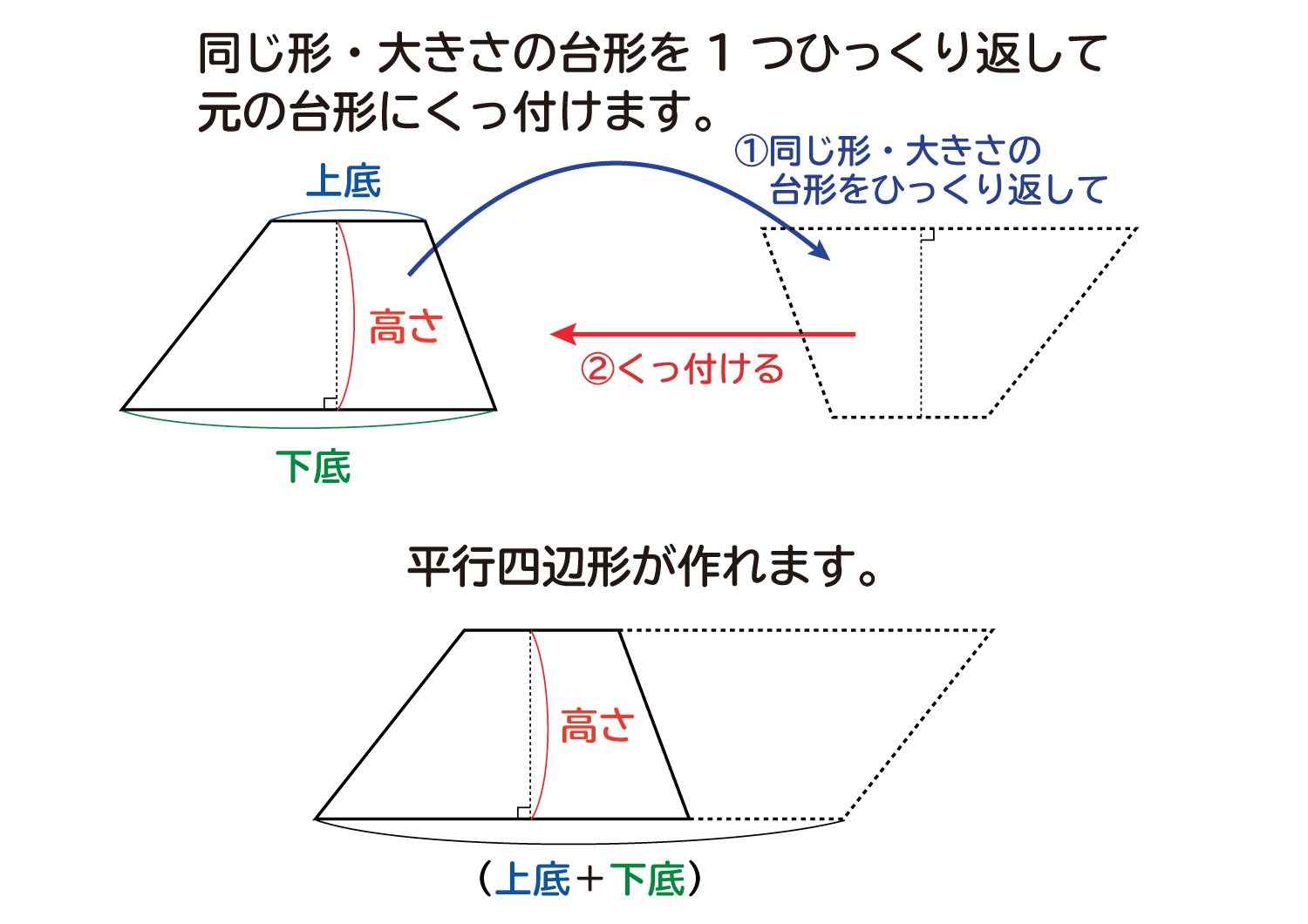



なぜ 台形の面積は 上底 下底 高さ 2 なのか を説明します おかわりドリル



平面図形の面積 A 周長 L および重心位置 G 台形 P11
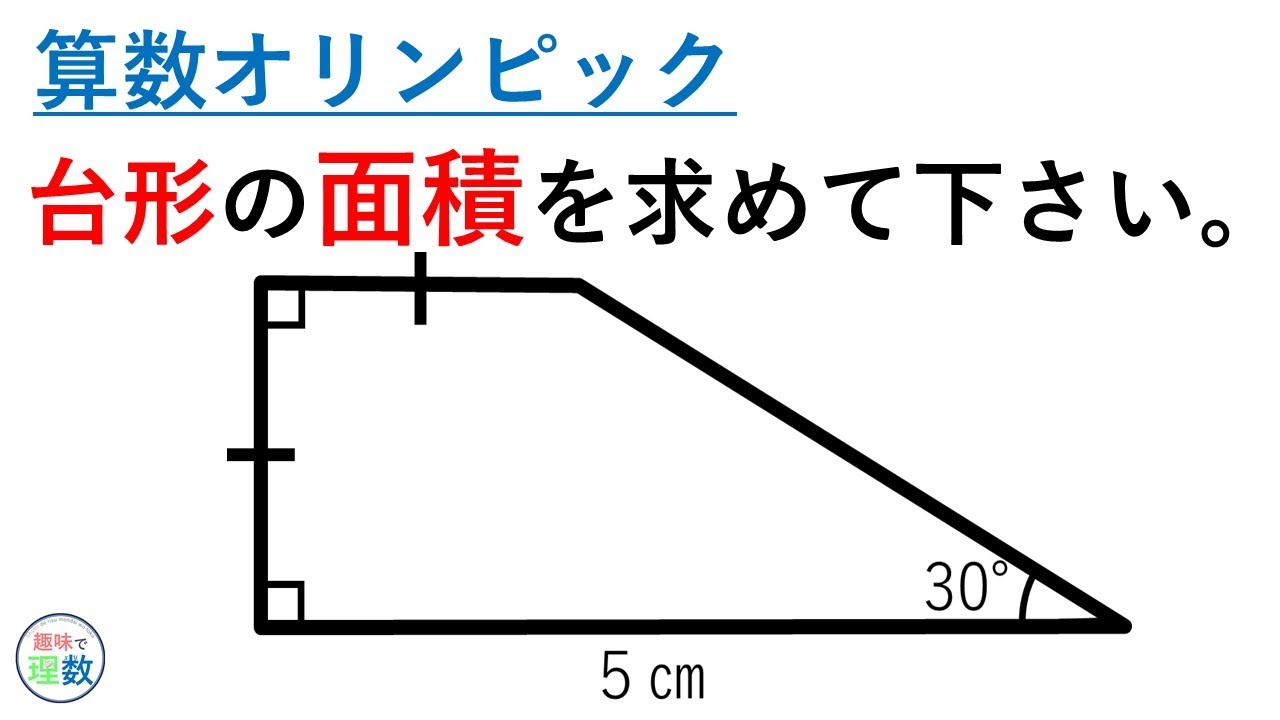



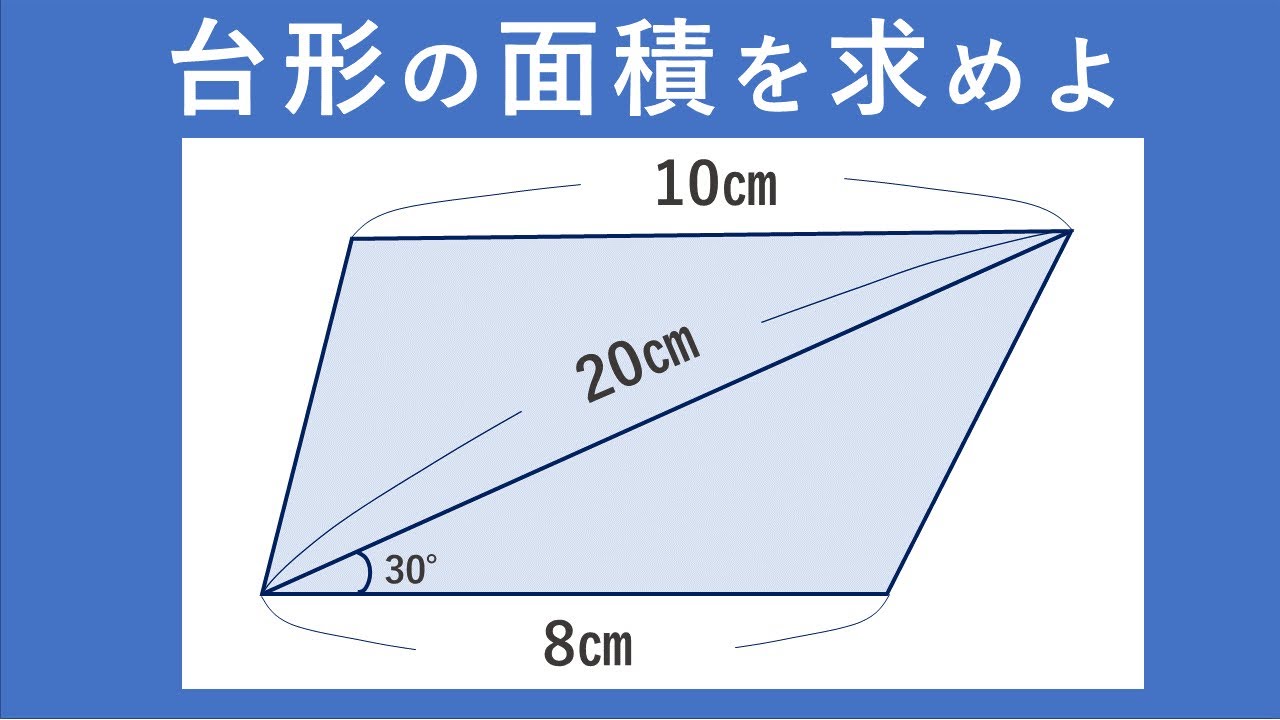
算数オリンピック 台形の面積を求めて下さい Youtube
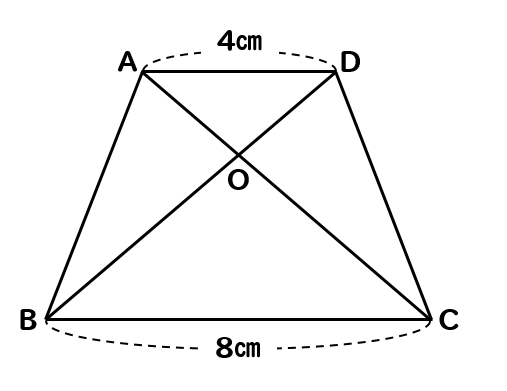



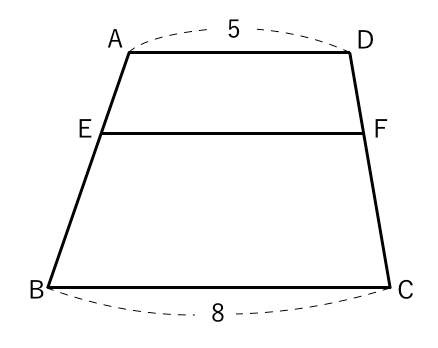
相似 台形と面積比の問題を徹底解説 数スタ




台形の面積の求め方 公式と計算例




四角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ
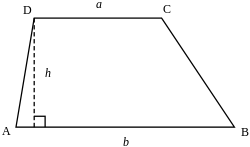



台形 Wikipedia



台形の面積と公式 面積計算機



面積分割




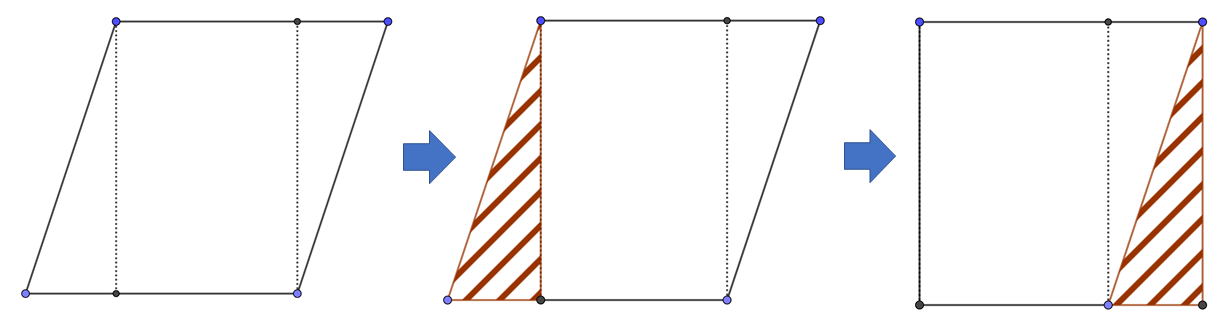
台形の面積の求めかたは 忘れても大丈夫 公式は自分でつくろう
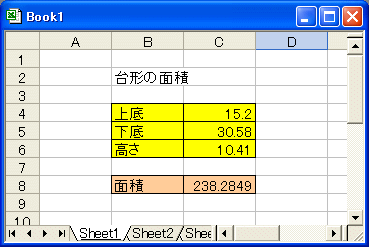



台形の面積を求めるexcelユーザー定義関数



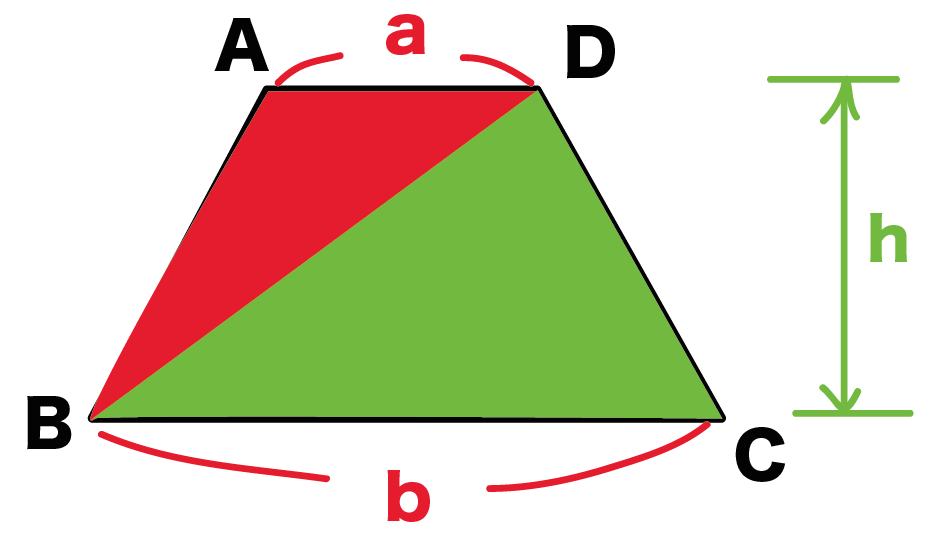
算数解法の極意 台形の面積比は 青山学院中等部 2012年 算数解法の極意




台形の面積は公式が分からなくても大丈夫 対角線を引いたり等積変形を利用したりする求め方とは みけねこ小学校
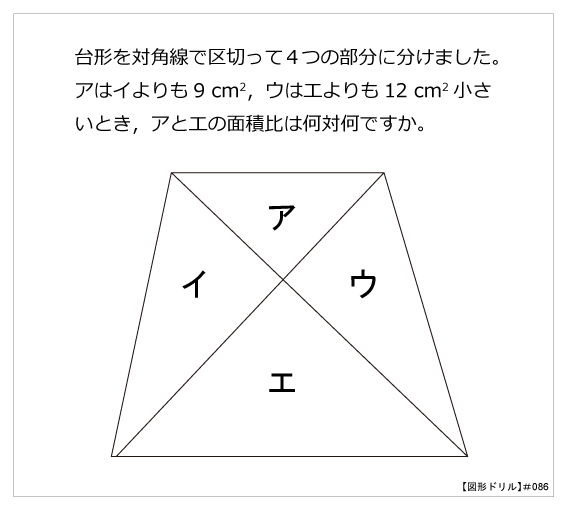



図形ドリル 第86問 台形の面積比 算数星人のweb問題集 中学受験算数の問題に挑戦



C言語アルゴリズム 台形面積近似による数値積分 Tsuneラボ 実験記録



台形 面積の計算 計算サイト




小5算数 図形の面積 指導アイデア みんなの教育技術



1
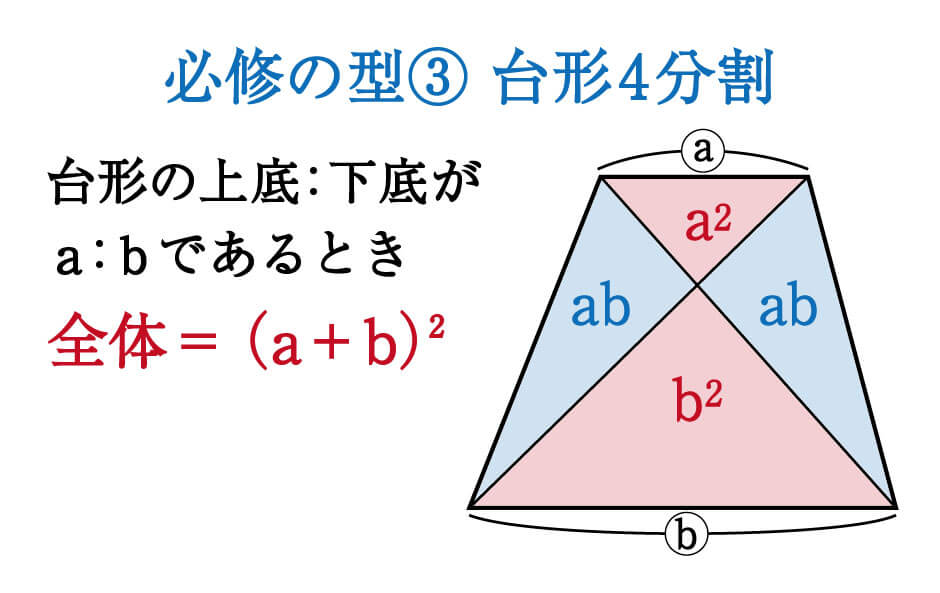



数学 台形を4分割した図形パターン 面積比 集中特訓 3 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
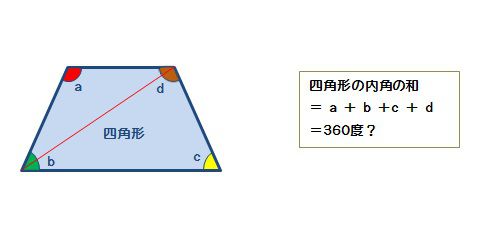



四角形の内角の和 算数の公式覚えてますか
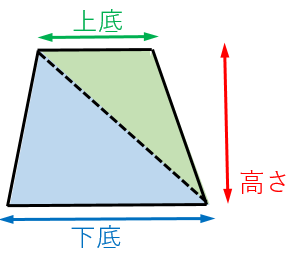



台形の面積を求める公式 具体例で学ぶ数学



台形の底辺は 1分でわかる意味 計算 求め方 上辺 面積との関係



面積を二等分する直線 高校受験のための数学
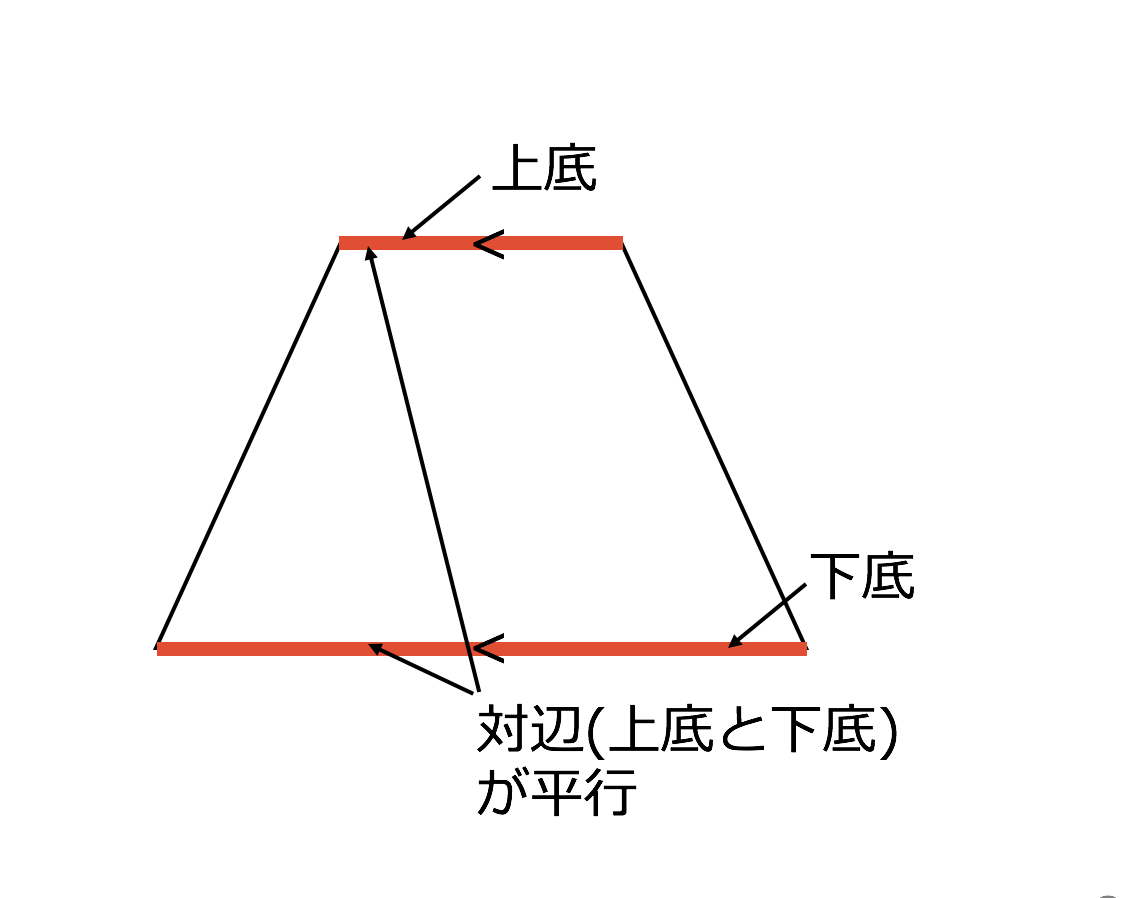



3分で分かる 台形の面積の求め方 公式についてわかりやすく 合格サプリ




台形ねじ 技術情報 Misumi Vona ミスミ
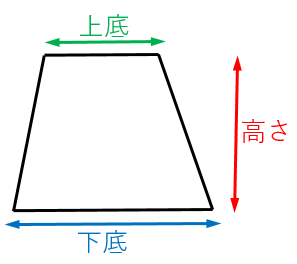



台形の面積を求める公式 具体例で学ぶ数学



1
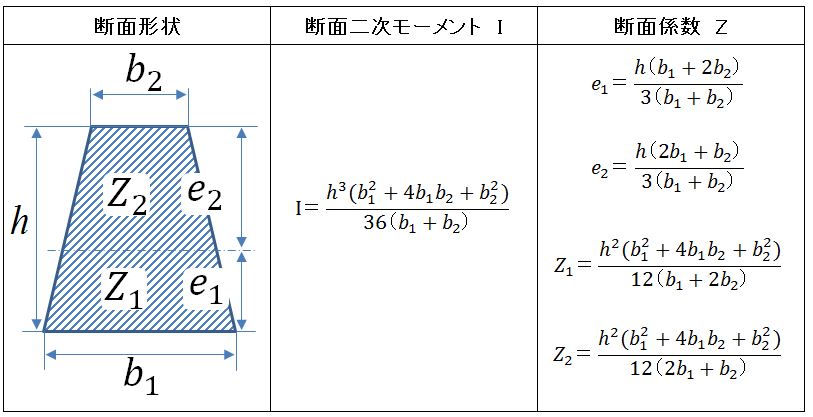



断面二次モーメント 断面係数の計算 台形 製品設計知識
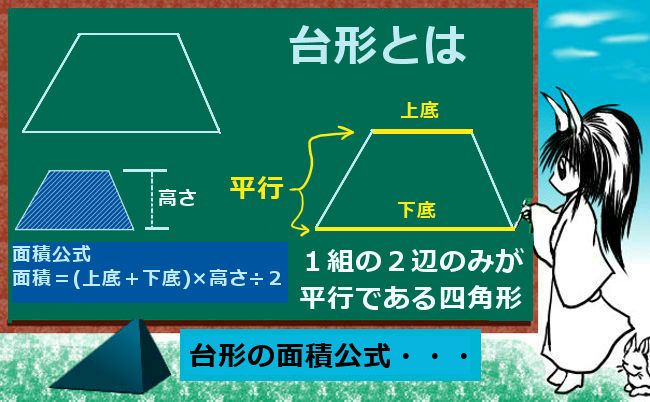



台形の面積公式 算数と図形 理数系無料オンライン学習 Kori




台形の面積




Excelによる積分 Ppt Video Online Download
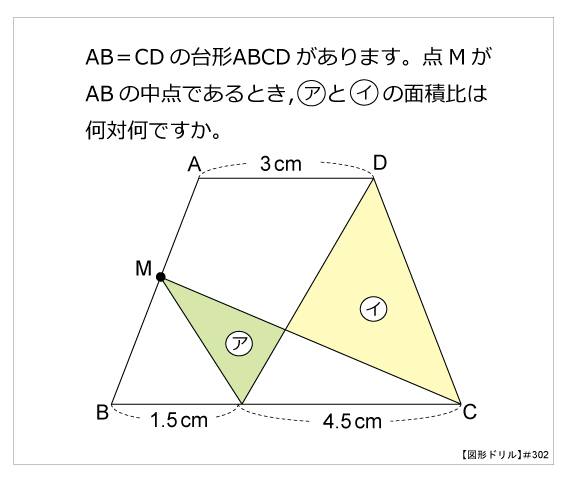



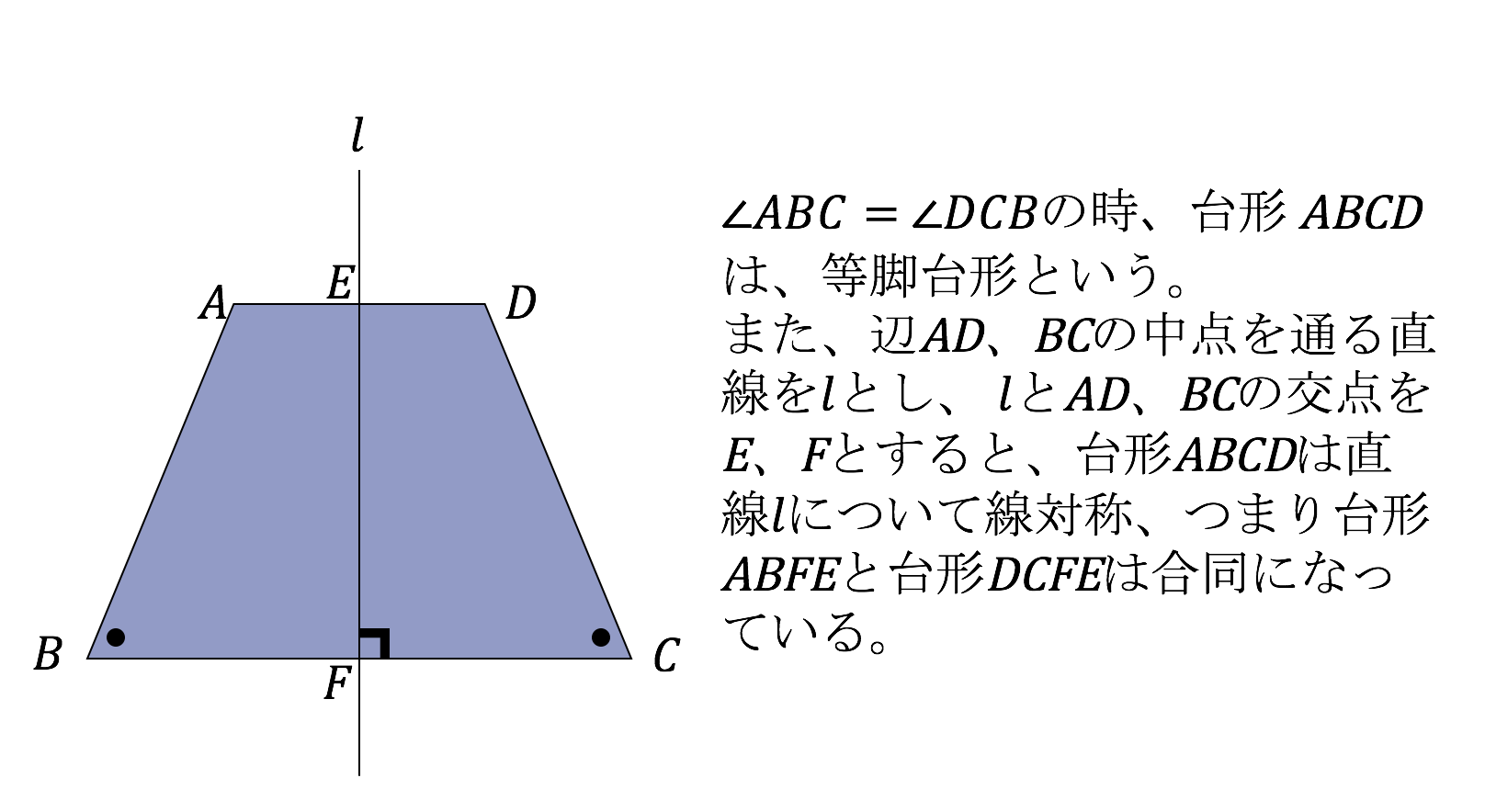
図形ドリル 第302問 等脚台形と面積比 算数星人のweb問題集 中学受験算数の問題に挑戦
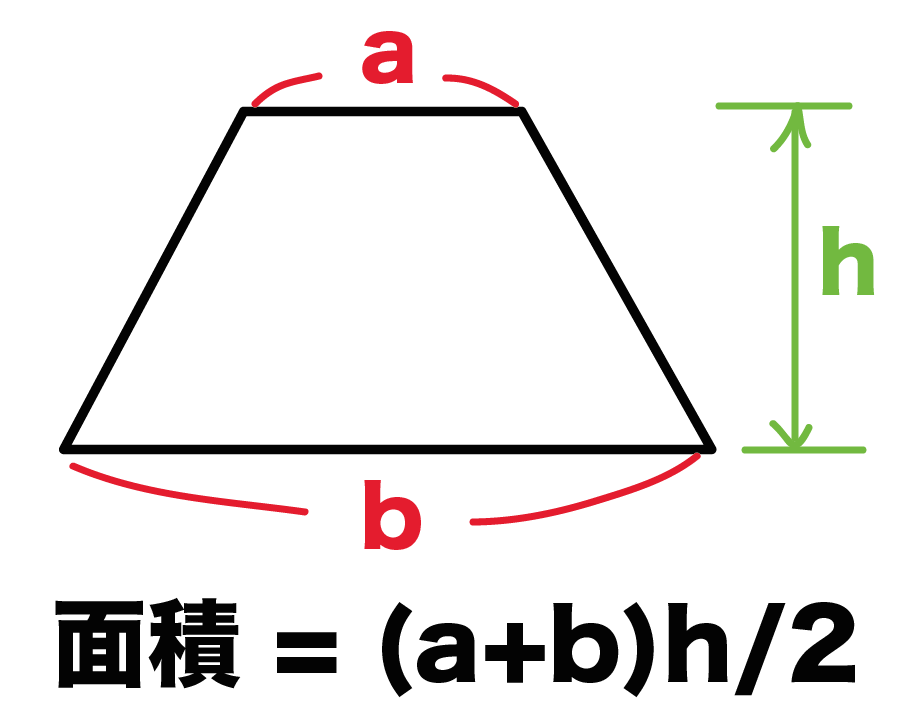



簡単公式 台形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



なぜ 台形の面積は 上底 下底 高さ 2 なのか を説明します おかわりドリル



簡単公式 台形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




台形の 面積 底辺 角度 から 上辺と高さ の求め方 台形の面積 数学 教えて Goo



Excel エクセルで台形の面積を計算する方法 モッカイ



台形の底辺は 1分でわかる意味 計算 求め方 上辺 面積との関係



台形の面積 計算機 基本公式と高さが分からないときの求め方 やまでら くみこ のレシピ




台形の面積の求め方 公式と計算例




台形の面積を求める方法 8 ステップ 画像あり Wikihow



台形の面積の計算を教えてください 別添図のような 台形で上底の数値が決まってお Yahoo 知恵袋



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典



台形の面積の公式 Youtube




よく出る台形の面積比 算数 過去問で基本を鍛える 12 勉強法のバイブル 帝都大学へのビジョン



図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師



3分で分かる 台形の面積の求め方 公式についてわかりやすく 合格サプリ
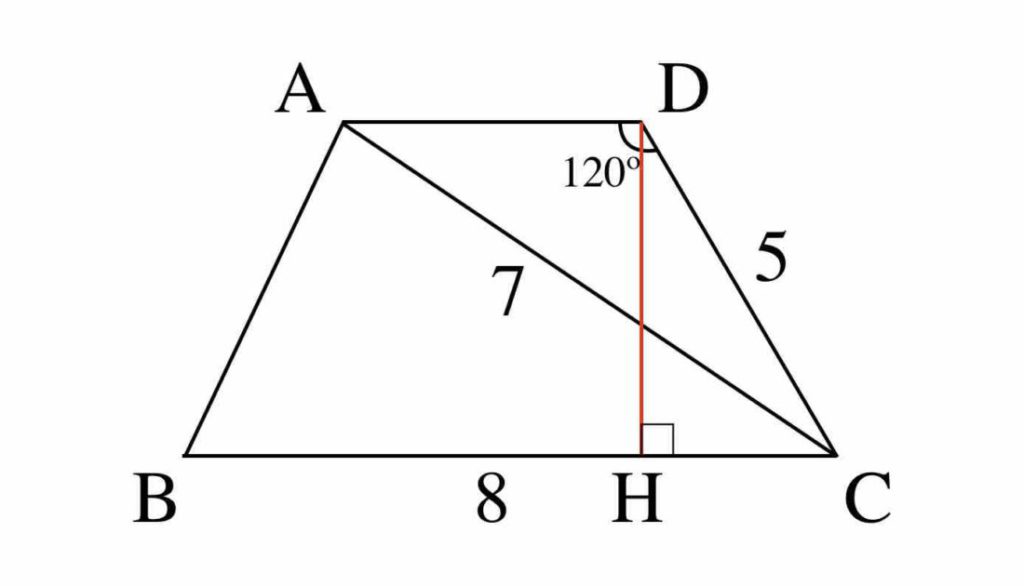



三角比を用いた面積計算をマスターしよう スタディクラブ情報局



面積分割
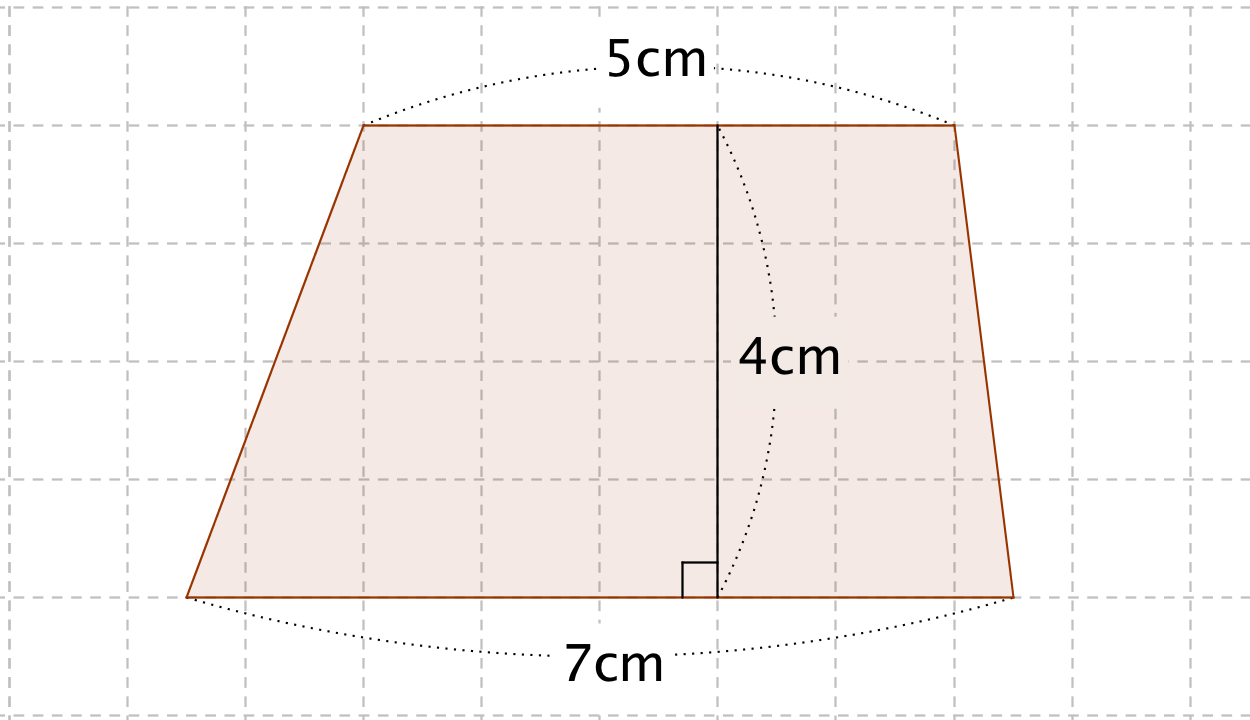



台形の面積の公式 算数の公式




台形 の面積 計算ドリル 問題集 数学fun
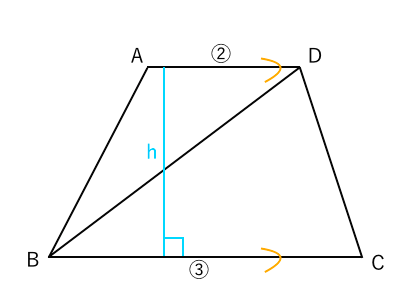



簡単に面積が何倍か求められる 使える編 苦手な数学を簡単に



1
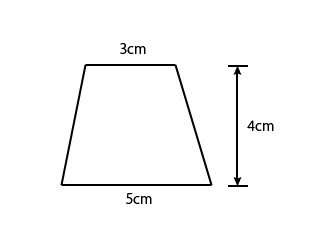



台形の面積の計算 もう一度やり直しの算数 数学
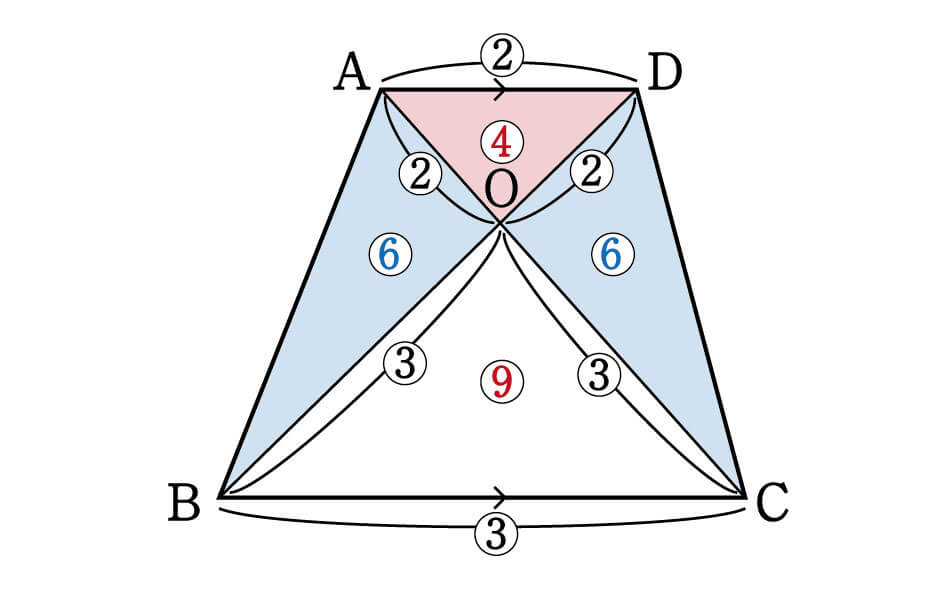



数学 台形を4分割した図形パターン 面積比 集中特訓 3 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
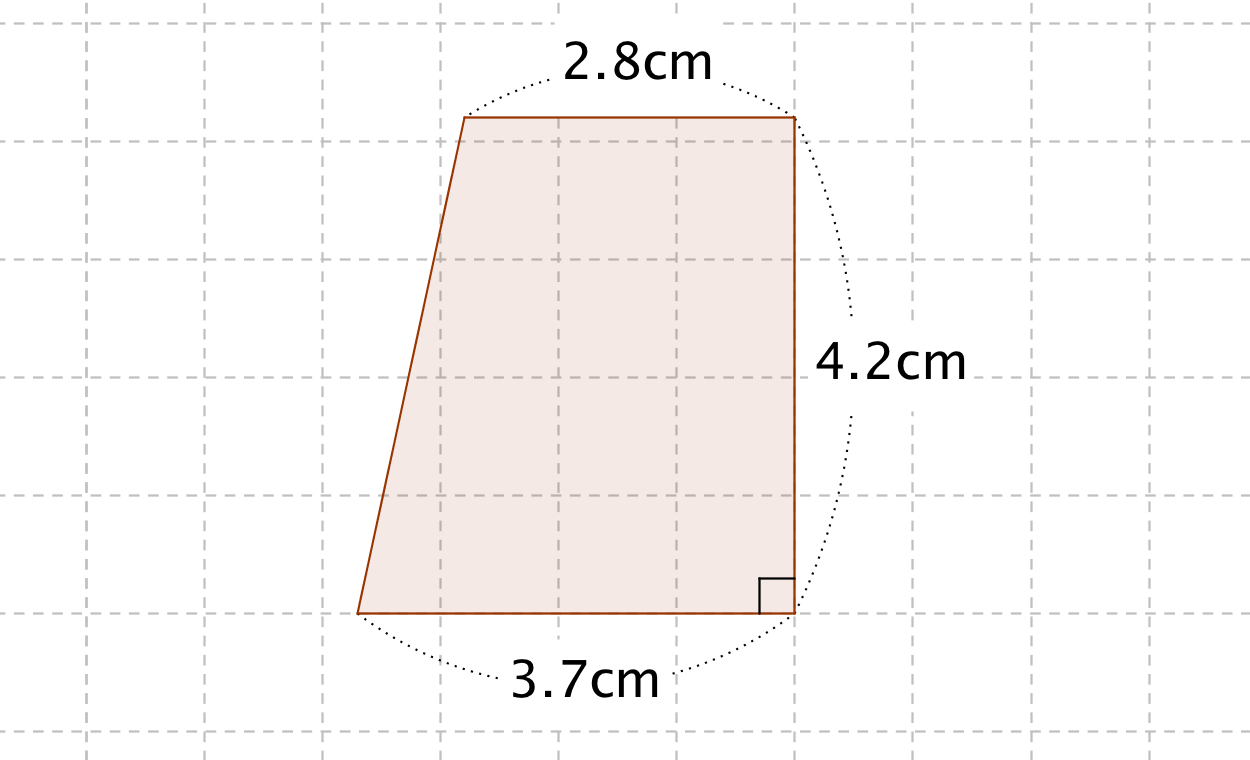



台形の面積の公式 算数の公式



0 件のコメント:
コメントを投稿